In the row of "original drive", we have the first part of the travel, so the time needed was 8 hours. The distance can be found by multiplying the rate and the time:
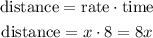
Then, in the "return drive", the rate is 9 mph higher, so the rate is "x + 9".
Also, the time is 7 hours. So, the distance is:
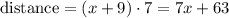
Since the distances are the same, we can write the following equation and solve it for x:
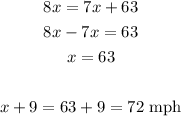
Therefore the average speed on the return drive is 72 mph.