Question

Can you help me write 2 expressions that is equal to the length of side BC..?

Answer 1

The diagram represents a right-angled triangle and we are given the following sides

AB=6

AC=4.9

BC=?

METHOD 1

We can write an expression for BC using the Pythagoras theorem below:

`\begin{gathered} AB^2=AC^2+BC^2 \\ BC^2=AB^2-AC^2 \\ BC=\sqrt[]{AB^2-AC^2} \end{gathered}`

Therefore the expression is

`BC=\sqrt[]{AB^2-AC^2}`

The expression can be further solved to get BC

`\begin{gathered} AB^2=AC^2+BC^2 \\ 6^2=4.9^2+BC^2 \\ 36=24.01+BC^2 \\ BC^2=36-24.01 \\ BC^2=11.99 \\ BC^2=\sqrt[]{11.99} \\ BC=3.46 \\ \end{gathered}`

METHOD 2

The second expression can be gotten using SOHCAHTOA:

Since we are given the opposite side and the hypotenuse we would make use of

CAH

`\begin{gathered} \cos \theta=\frac{\text{Adj}}{Hyp} \\ \cos \theta=(BC)/(6) \\ cross\text{ multiply} \\ BC=6\cos \theta \end{gathered}`

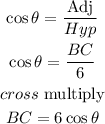
Therefore the expression is

`BC=6\cos \theta`

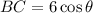
The expression can be further solved to get BC

`\begin{gathered} BC=6\cos 55 \\ BC=6*0.5736 \\ BC=3.44 \end{gathered}`

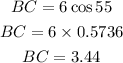
We can clearly see that both methods give a very similar answer. Therefore the expressions are correct