Question

Find the area of a regular octagon with a side length of 4m.

Answer 1

First, draw the octagon

the formula of area of an octagon is

`A=4* a_p* L`

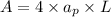
where L is a side(4m) and we need to find the value of ap, then we can take the triangle

we use tangent to solve

`\tan (\alpha)=(O)/(A)`

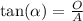
where alpha is the reference angle, O the opposit side of the reference angle and A the adjacent side of the reference angle

if the reference angle is 135/2 we replace

`\tan ((135)/(2))=(a_p)/(2)`

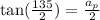
and solve for ap

`\begin{gathered} a_p=2\tan ((135)/(2)) \\ a_p_{}=4.83 \end{gathered}`

now we replace the values on the formula of the area of the octagon

`\begin{gathered} A=4* a_p* L \\ A=4*4.83*4 \\ A=77.28 \end{gathered}`

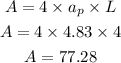
then the area of the octagon is 77.28 square meters