Question

From the diagram below, if PD = 3, DC = 2, and BC = 4, is AC a tangent line? (Hint: PB and PD are both radii !!)

Answer 1

Given:

In the given diagram,

`PD=3,DC=2,\text{ }and\text{ }BC=4`

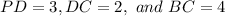
To check:

AC a tangent line or not.

Step-by-step explanation:

In a triangle PBC,

`\begin{gathered} PB=3\text{ }(Since\text{ }PB=PD=radius) \\ BC=4 \\ PC=3+2=5 \end{gathered}`

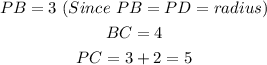
Let us check the Pythagoras theorem,

`\begin{gathered} PC^2=PB^2+BC^2 \\ 5^2=3^2+4^2 \\ 25=9+16 \\ 25=25 \end{gathered}`

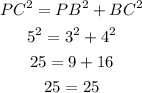
It satisfies the theorem.

Therefore, the triangle PBC is a right-angle triangle.

That is, PB is perpendicular to AC.

So, AC is a tangent line.

Final answer:

Yes. AC is a tangent line.