Question

Raya set up a short scavenger hunt using matrices to encode the location of a wooden token. The scavenger hunt might involve several locales on the school campus, such as the auditorium, cafeteria, gymnasium, library, and the quad (common area where students gather). To receive the first clue, Darnell has to first encode a message to Raya.To encode the message, Darnell was given a 2 x 2 encoding matrix, A. Each letter of the alphabet is assigned a numerical value, and the value ‘0’ represents a space and is indicated in the code by an underscore ( _ ). 0_ 9I18R1A10J19S2B11K20T3C12L21U4D13M22V5E14N23W6F15O24X7G16P25Y8H17Q26ZThe method in which the messages are encoded is as follows.“Test one” coordinates to the number string: 20 5 19 20 0 15 14 5TEST_ ONE2051920015145The encoding matrix is 2 x 2, so the enumerated message above is broken up into a sequence of 2 x 1 matrices, then combined to create matrix M. The encoded matrix is the result of matrix multiplication between the coded matrix, A, and the enumerated message, M. Recall that in order to start the scavenger hunt, Darnell needs to send an encoded message to Raya.a)Based on the table, what is the number string that corresponds to the text “Hello Raya”? (1 point)b)How many 2 x 1 matrices will be in the sequence? How do you know that? (2 points)c)Write the sequence of 2 x 1 matrices that Darnell will use to encode. (1 point)d)What is the enumerated matrix B? (2 points)e)What is A × B? (Show your work)

Answer 1

a) The text 'Hello Raya', once coded, is,

`\begin{gathered} H=8,E=5,L=12,L=12,O=15,0=space,R=18,A=1,Y=25,A=1_{} \\ 8,5,12,12,15,0,18,1,25,1 \end{gathered}`

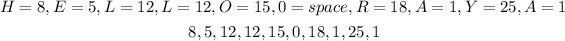
b) The number string in part a) consists of 10 numbers, and we need to divide those into 2x1 matrices. Therefore, we can make 5 2x1 matrices with 10 numbers. The answer is 5 matrices.

c) The 5 2x1 matrices are

Suppose matrix B has the following form

`\begin{gathered} B=\begin{bmatrix}{b_1} & {b_2} & {\ldots} \\ {} & {} & {} \\ {} & {} & {}\end{bmatrix} \\ \text{where} \\ b_i\to2*1\text{ matrix} \end{gathered}`

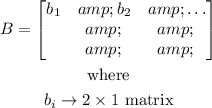
Therefore, in our case, B is

e) Finally, for the product of matrices A and B to be valid, we need to define it like shown below

`A* B=\begin{bmatrix}{A* b_1} & {A* b_2} & {\ldots} \\ {} & {} & {} \\ {} & {} & {}\end{bmatrix}`

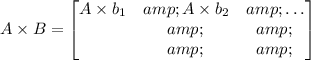
Thus,