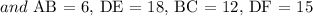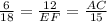SOLUTION:
Step 1:
In this question, we are given the following:
ABC is similar to DEF.
The measure of AB = 6,
the measure of DE = 18,
the measure of BC = 12,
and the measure of DF = 15.
Find the measures of AC and EF.
Step 2:
The details of the solution are as follows:
![\begin{gathered} Since\text{ ABC }\cong\text{ DEF} \\ This\text{ means that:} \\ (AB)/(DE)=(BC)/(EF)=(AC)/(DF) \end{gathered}]()