Question

The function f(x)=−18sin(0.5x + 16) - 3 models the average rate of change in temperature of a substance monitored in an experiment. In the function, x represents the number of minutes since the commencement of the experiment and the temperature of the substance is measured in degrees Fahrenheit.Over what range of temperatures does the average rate of change in temperature fall?

Answer 1

given the function

`f(x)=-18sin(0.5x+16)-3`

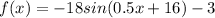
x = minutes

f(x)= rate of change in temperature

sin(x) function find his highest when

`x=(\pi)/(2)`

sin(pi/2)=1

then we need to solve

`0.5x+16=(\pi)/(2)`
`0.5x=(\pi)/(2)-16`
`x=-28.85`

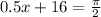
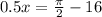
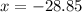
then when x=-28.85 sin(0.5x+16) = 1

then

`f(x)=-18*(1)-3`
`f(x)=-21`

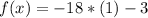
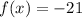
we just find the lowest value of the function

now we need to find the highest value of the function

Remember the highest value of the function is not the highest value of sin, this is not related

Now, we have to do a similar process but insted of solving

sin(x)=1 we are trying to solve

sin(x)=-1

`0.5x+16=(3)/(2)\pi`
`x=-22.57`

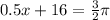
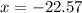
then when x=-22.57 sin(x)=-1

then

`f(x)-18*(-1)-3`

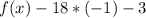
f(x)= 18-3= 15

then the range of temperatures are

lowest at -21

highest at 15

little tip, sin(x)=1 every n*pi/2 when n is odd

little tip, sin(x)=-1 every n*pi/2 when n is even

sin(x)= 0 when every pi