Question

I need help with trigonometry , this is the stuff im learning but i don’t know how to do anything i havent payed attention in class

Answer 1

We have to solve for x:

`(\sin(54.6\degree))/(x)=(\sin(87\degree))/(16.8)`

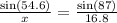
We can rearrange to do a cross multiplication. When we have a proportion like this, we can do cross multiplication like this:

`(a)/(b)=(c)/(d)\Longrightarrow a\cdot d=c\cdot b`

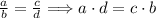
Each side will be the product of the numerator in that side and the denominator of the other side. This is just the application of the property of the multiplication and division.

In this case, we apply this cross multiplication as:

`\begin{gathered} (\sin(54.6\degree))/(x)=(\sin(87\degree))/(16.8) \\ \sin (54.6\degree)\cdot16.8=\sin (87\degree)\cdot x \end{gathered}`

From the final equation, we can divide both sides by sin(87°):

`\begin{gathered} \sin (54.6\degree)\cdot16.8=\sin (87\degree)\cdot x \\ (\sin (54.6\degree)\cdot16.8)/(\sin (87\degree))=(\sin(87\degree)\cdot x)/(\sin(87\degree)) \\ (\sin(54.6\degree)\cdot16.8)/(\sin(87°))=x \end{gathered}`

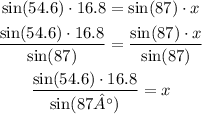
Solving this we get:

`\begin{gathered} x=(\sin(54.6\degree)\cdot16.8)/(\sin(87\degree)) \\ x\approx(0.815\cdot16.8)/(0.999) \\ x\approx(13.692)/(0.999) \\ x\approx13.7 \end{gathered}`

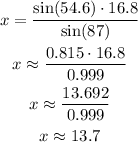
Answer: x = 13.7

NOTE:

After a cross multiplication, we can solve for any variable.

For example, if we want to solve for the variable "b", we can do like this:

`\begin{gathered} (a)/(b)=(c)/(d) \\ a\cdot d=c\cdot b \\ (a\cdot d)/(c)=(c\cdot b)/(c) \\ (a\cdot d)/(c)=b \end{gathered}`

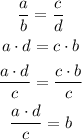
Now we know that b is equal to (a*d)/c.

The third step is just divide both sides of the equation by the same factor. In this case, we select c in order to have b alone in one side of the equation.