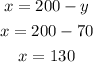130 ml of solution 1 and 70 ml of solution 2
Explanation
Step 1
Let
Volume of solution 1 ( 20% saline solution)=x
Volume of solution 2( 60 % saline solution)=y
Step 2
replace
Theodore needs to mix a 20% saline solution with a 60% saline solution to create 200 milliliters of a 34% solution
the volume of salt ( in solution 1)= 0.2 *volume of the solution 1
the volume of salt ( in solution 2)= 0.6 *volume of the solution 1
the volume of salt ( in mix)= 0.34 *volume of mix
replace,
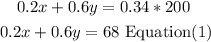
Also
volume os solution 1 + volume of solution 2 = volume of mix
replace,
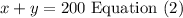
Step 3
use equatino (1) and (2) to find x and y
a) isolate x form equation (2)
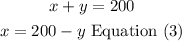
b) replace equation (3) in equation (1)

c) replace the valur of y =70in equation (3) to find x