Question

Find the total surface area & volume of figure in image

Answer 1

The given solid is the frustum of a cone. It is a part of a complete cone. The complete cone is shown below

Volume of frustum = volume of cone ABC - volume of cone FGC

Recall, the formula for finding the volume of a cone is expressed as

Volume = 1/3 x pi x radius^2 x height

Triangle EBC is similar to triangle DGC. This means that

h/25 + h = 5.5/8.5

By crossmultiplying,

8.5h = 5.5(25 + h) = 137.5 + 5.5h

8.5h - 5.5h = 137.5

3h = 137.5

h = 137.5/3 = 45.83

height of complete cone = 25 + 45.83 = 70.83

Volume of big cone(ABC) = 1/3 x 3.14 x 8.5^2 x 70.83 = 5356.28

Volume of small cone(FGC) = 1/3 x 3.14 x 5.5^2 x 45.83 = 1451.05

Volume of frustum = 5356.28 - 1451.05 = 3905.23

The formula for the total surface area is expressed as

`\text{Total surface area = piL(r + r') + pi}* r^2\text{ + pi}* r^(\prime2)`

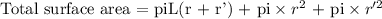
L is the slant height of the frustum

r' is the radius of cone FGC

r is the radius of cone ABC

L = 25.9

r = 8.5

r' = 5.5

Total surface area = 3.14 x 25.9(8.5 + 5.5) + 3.14 x 8.5^2 + 3.14 x 5.5^2

= 1138.564 + 226.865 + 94.985

Total surface area = 1460