Given Data:
*The speed of the plane is:

*The height from which the package is dropped is:
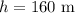
*The time at which the second package is dropped is:
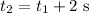
Here,
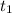
is the time at which the first package is dropped.
Step-by-step explanation:
The initial vertical velocity is:
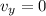
The acceleration of the motion in vertical y-axis is:
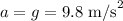
Using the kinematics equation, we get:
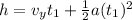
Substituting the known values, we get:
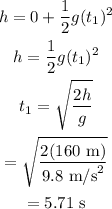
The displacement of the first package is:
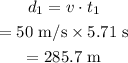
The time taken by the second package is:
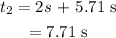
The displacement of the second package is:
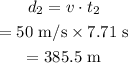
The distance between the two packages when they are both dropped on the ground is:
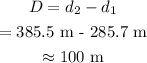
Final Answer:
The correct option is 100 m.