Question

Kurt says that if he starts with a number n, multiplies it by the next whole number, and then adds 3, he will get 45 .n(n+1)+3=45What number n makes Kurt's equation true?6785

Answer 1

n=6

Step-by-step explanation:

The equation which describes Kurt's problem is:

`n(n+1)+3=45`

We are required to solve for n.

`\begin{gathered} n(n+1)+3=45 \\ n(n+1)=45-3 \\ n^2+n=42 \\ n^2+n-42=0 \end{gathered}`

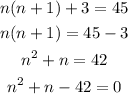
We then solve the quadratic equation obtained above by factorization.

`\begin{gathered} n^2+7n-6n-42=0 \\ n(n+7)-6(n+7)=0 \\ (n-6)(n+7)=0 \\ \implies n-6=0\lor n+7=0 \\ \implies n=6\lor n=-7 \end{gathered}`

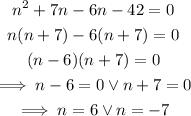
Since we are dealing with whole numbers, and -7 is not a whole number, we conclude that -7 is not a valid result.

The number, n which makes the equation true is 6.