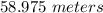Given the Quadratic Function:
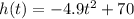
(a) You need to substitute this value of "t" into the function and evaluate:
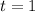
In order to find:
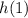
Then, you get:
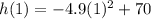
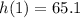
You need to substitute this value of "t" into the function and evaluate:

In order to find:
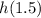
Then, you get:
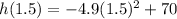
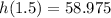
(b) You know that "h" represents the height of the ball after it is dropped (in meters) and "t" represents the time (in seconds) after it is dropped. Therefore:
1. Having this function value:
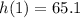
You can conclude that, after 1 second, the height of the ball is:
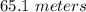
2. Having this function value:
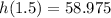
You can conclude that, after 1.5 seconds, the height of the ball is:
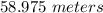
Hence, the answers are:
(a)
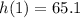
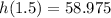
(b) - Interpretation for this function value:
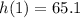
After 1 second, the height of the ball is:
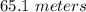
- Interpretation for this function value:
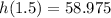
After 1.5 seconds, the height of the ball is: