Question

What is the component form of the vector whose tail is the point (−4,8), and whose head is the point (3,−6)?

Answer 1

It is given that a vector has a tail at point (-4,8) and a head at point (3,-6). It is required to find the vector in component form.

Recall that a vector, v with tail at the point (a,b) and head at the point (c,d) has the component form:

`\textbf{v}=\langle(c-a),(d-b)\rangle`

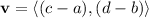
Substitute (a,b)=(-4,8) and (c,d)=(3,-6) into the component form:

`\textbf{v}=\langle(3-(-4)),(-6-8)\rangle=\langle(3+4),(-6-8)\rangle=\langle7,-14\rangle`

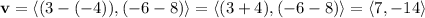
Hence, the required vector in component form is < 7, -14 >.

The required vector in component form is < 7, -14 >.