Let the rate of the plane in still air be v;
Let the rate of the plane with the wind be u;
Thus, when the airplane flies against the wind, we have;
![\begin{gathered} d=3920\operatorname{km},t=8\text{hours} \\ v-u=(3920)/(8) \\ v-u=490\ldots\ldots\ldots\ldots\text{equation 1} \end{gathered}]()
Also, when the same airplane flies with the wind, we have;
![\begin{gathered} d=5580\operatorname{km},t=6hours \\ v+u=(5580)/(6) \\ v+u=930\ldots\ldots\ldots\ldots\ldots\text{equation 2} \end{gathered}]()
Thus, we solve equation 1 and equation 2 simultaneously by subtracting equation 1 from equation 2. We have;
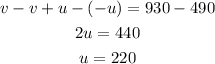
Thus, we substitute the value of u in equation 2, we have;
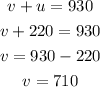
Hence, the rate of the airplane in still air is 710km/hour and the rate of the airplane with the wind is 220km/hour.