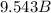1 Answer

Ask a Question

Gadoma · Answer 1 · 2023-11-02T09:50:56+0000

Answer:

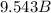
Step-by-step explanation: We have to find the world population in the year 2046, the formula for the population is as follows:

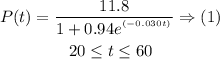
$\begin{gathered} P(t)=\frac{11.8}{1+0.94e^{^((-0.030t))}}\Rightarrow(1) \\ 20\leq t\leq60 \end{gathered}$

The year 2046 translates to:

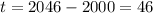
Therefore the population would be:

$\begin{gathered} \Rightarrow P(46)=(11.8)/(1+0.94e^((-0.030*46))^)\operatorname{\Rightarrow}(1) \\ \Rightarrow P(t)=(11.8)/(1+0.94e^(-1.38))=(11.8)/(1+(0.94)/(e^((1.38)))) \\ \Rightarrow P(46)=9.543 \end{gathered}$

Therefore the population in 2046 would be as follows:

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions