The Quadratic formula is:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Given the Quadratic equation:
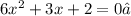
You can see that it has this form:
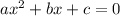
Then, in this case:
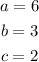
Therefore, you can substitute values into the Quadratic formula:
![x=\frac{-(3)\pm\sqrt[]{(3)^2-4(6)(2)}}{(2)(6)}](https://img.qammunity.org/2023/formulas/mathematics/college/1wom0obl9m0hy9i9nt6fxu7ykkoio5rtjr.png)
Evaluate:
![\begin{gathered} x=\frac{-3\pm\sqrt[]{^{}-39}}{12} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mmzybymby95z6d0j6rck3qjyy36vimge10.png)
Notice that the Radicand (the value inside the root) is negative.
By definition:
![i=\sqrt[]{-1}](https://img.qammunity.org/2023/formulas/mathematics/college/prwnjpkamd054mvqxx3wkz9peqbswm21lz.png)
Then you can rewrite it in this form:
![x=\frac{-3\pm i\sqrt[]{^{}39}}{12}](https://img.qammunity.org/2023/formulas/mathematics/college/ibrhvjj5uol28fvur1n9qz142gzquqp68r.png)
Therefore, you get that the answer is:
![\begin{gathered} x_1=\frac{-3-i\sqrt[]{^{}39}}{12} \\ \\ \\ x_2=\frac{-3+i\sqrt[]{^{}39}}{12} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8cq5q27pf6im779m15sumfokruwfa62ass.png)