The sequence is not an arithmetic sequence because. The n-term for an arithmetic sequence is:
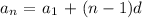
where d is the difference between two consecutive numbers. In this case d = 2. Because
15-13 = 2
13-11 = 2
11- 9 = 2
now, the first term for 15,13,11,9 is 15 = a_1, the second term would be:

that is equivalent to say:
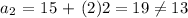
So we can conclude that 15,13,11,9 is not an arithmetic sequence.