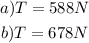Question

Suppose a 60.0-kg gymnast climbs a rope. (a) What is the tension in the rope if he climbs at a constant speed? (b) What is the tension in the rope if he accelerates upward at a rate of 1.50 m/s2?

Answer 1

Use the Newton's Second Law of Motion to find the tension in the rope on each case.

a)

Since the gymnast climbs at a constant speed, then the net force acting on the gymnast must be 0. Since there are only two forces acting on the gymnast, namely the tension of the rope and the weight of the gymnast, then:

`\begin{gathered} F_N=T-W=0 \\ \Rightarrow T=W \end{gathered}`

On the other hand, the weight of the gymnast is equal to the product of its mass times the acceleration of gravity, g=9.81m/s^2:

Then, the tension of the rope is:

`T=588N`

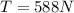
b)

The forces acting on the gymnast are 2: the tension of the rope and the gravitational pull:

`F_N=T-W`

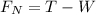
From the second law of motion, we know that the net force acting over an object of mass m produces an acceleration a given by:

`F_N=ma`

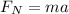
Then:

`\begin{gathered} T-W=ma \\ \Rightarrow T=W+ma \end{gathered}`

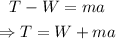
Substitute W=588N, m=60kg and a=1.50 m/s^2 to find the tension of the rope:

Therefore, the answers are:

`\begin{gathered} a)T=588N \\ b)T=678N \end{gathered}`