Given: A farmer is going to divide her40 acre farm between two crops
To Determine: How many acres of each crop should the farmer plant to maximize her profit
Solution
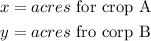
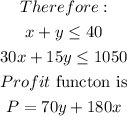
The graph of the inequalitiesis as shown below
Neglecting the negative axis, the point that will maximize the profit are te points shown above with their coordinates
The coordinates will maximum profits are
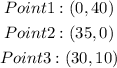
Substitute the 3 points into the profit functions to determine thepoint that will given the maximum profit
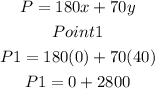
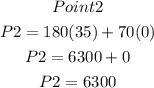
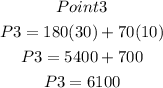
Hence, the point that will maximize profit is (35, 0), which is
35 acres of crop A, and
0 acre of crop B