To determine the x- and y-intercepts is best to write the equation in slope-intercept form.
Given

-Pass the x-term to the right side of the equation by applying the opposite operation to both sides of it:
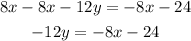
-Divide both sides of the equal sign by -12
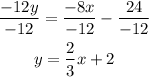
So the equation in slope-intercept form is:
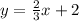
a) The x-intercept is the point where the line crosses the x-axis, at this point, the y-coordinate is equal to zero. To determine the x-coordinate of the intercept, you have to equal the equation to zero and calculate the corresponding value of x:
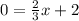
-Subtract 2 to both sides of the equal sign

-Multiply both sides of the expression with the reciprocal fraction of 2/3
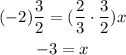
The x-intercept is (-3,0)
b) The y-intercept is the point where the line crosses the y-axis, at this point, the x-coordinate is equal to zero. To determine the y-intercept, replace the equation with x=0 and calculate the corresponding value of y:
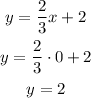
The y-intercept is (0,2)
c) To graph the line, plot both intercepts on the coordinate system and then link both points with a line: