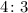Answer:
The ratio of the high-wire unicyclists to ball-balancing seals is;
Step-by-step explanation:
Given that;
He has featured 32 high-wire unicyclists and 24 ball-balancing seals.
The ratio of the high-wire unicyclists to ball-balancing seals can be written as;
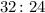
Reducing toits lowest form, we have;
divide both sides by 8;
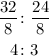
Therefore, the ratio of the high-wire unicyclists to ball-balancing seals is;