Let p be the total linear momentum of the system before the collision and p' the total linear momentum of the system after the collision. Let p₁₁ and p₁₄ be the linear momentum of the 11.0kg ball and the 14.0kg ball before the collision, and let p₁₁' and p₁₄' be their linear momenta after the collision.
According to the Law of Conservation of Linear Momentum, the total linear momentum of the system before and after the collision remains the same. Then:
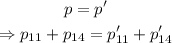
Let v be the unknown speed of the 11.0kg ball after the collision. Find the value of p₁₁, p₁₄, and p₁₄'. Find an expression for p₁₁' in terms of v and replace all the values into the above equation. Solve for v.
The linear momentum of a particle with mass m and velocity v is:
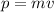
Then:

Then:

Therefore, the velocity of the first ball after the collision is 20.4m/s.