Question

Let f(a) = x^2 + 5.a) Find the y-value when x = 0.The y-value, output value is ___b) Find the y-intercept, when x = 0.The y-intercept is ___c) Find the x-values, when y = 46.The x-values are ____

Answer 1

To solve a, we need to replace x = 0 in the formula of the function:

`\begin{cases}f(x)=x^2+5 \\ x=0\end{cases}\Rightarrow f(0)=0^2+5=5`

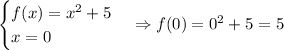
The y value when x = 0 is 5.

b is asking the same as a but in a different way. The y-intercept of a function is when x = 0, we just calculated that. The point of y-intercept is (0, 5)

Finally, to solve c, we need to find the values of x that gives us a value of f(x) = 46:

`f(x)=46\Rightarrow46=x^2+5`

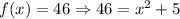
Then solve:

`\begin{gathered} x^2=46-5 \\ x=\pm\sqrt[]{41} \end{gathered}`

Remember that we must that plus-minus the value when we take square root. ± √41 is the answer to c.