Question

Hello, may I please have some help on this practice question? Thank you.

Answer 1

Data:

• p1 = ,the proportion of Republican voters in the first state

,

• p2 =, the proportion of Republican voters in the second state

,

• P1 = ,the proportion of Republican voters in the sample from the first state

,

• P1 = ,the proportion of Republican voters in the sample from the second state

,

• n = ,sample

Procedure

0. Finding the mean proportions

`p_1-p_2=0.52-0.47=0.05`

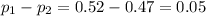
2. Finding the standard deviation of the difference

`\sigma=\sqrt[]{(0.52\cdot(1-0.52))/(100)+(0.47\cdot(1-0.47))/(100)}=0.0706`

To have a greater percentage of republicans in the second state than in the first, the difference should be less than zero. Thus, the value of the difference of the proportion corresponds to zero.

`Z=(0-0.05)/(0.0706)=-0.7080`

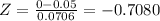
Using the Standard Normal Table, the value of Z previously calculated corresponds to 0.2394.

Therefore, the probability that the survey will show a greater percentage of Republican voters in the second state than in the first state is 0.24.

Answer: C) 0.24