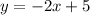Question

3 math questions multiple choice

Answer 1

1) the equation is:

`2y+x=4`

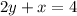
So we can rewrite the equation as a slope intercept so:

`\begin{gathered} 2y=-x+4 \\ y=-(1)/(2)x+2 \end{gathered}`

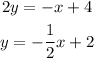
So the slope is -1/2

2) the equation is:

`3x-2y=5`

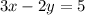
Now we evaluete the coordinates to see which one is not on the line so for (1,-1)

`\begin{gathered} 3(1)-2(-1)=5 \\ 3+2=5 \\ 5=5 \end{gathered}`

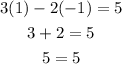
So is on the line

for (-1,-4)

`\begin{gathered} 3(-1)-2(-4)=5 \\ -3+8=5 \\ 5=5 \end{gathered}`

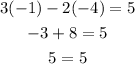
So it is on the line

for (3,2)

`\begin{gathered} 3(3)-2(2)=5 \\ 9-4=5 \\ 5=5 \end{gathered}`

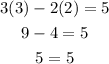
So it is on the line

Finally for (1,2)

`\begin{gathered} 3(1)-2(2)=5 \\ 3-4=5 \\ -1\\e5 \end{gathered}`

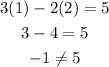
So (1,2) is not on the line

3) if the slope is -2 and goes to the point (3,-1) we can use the equation of a line to find the intercept so:

`\begin{gathered} y=-2x+b \\ -1=-2(3)+b \\ -1=-6+b \\ -1+6=b \\ 5=b \end{gathered}`

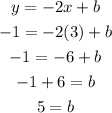
So the intercept is 5 so the equation is:

`y=-2x+5`