hello
to solve this question, we have to use trigonometric ratios and in this case, it was specified to use tangent
from the image above, we can see that we have the value of angle and opposite and we need to look for adjacent
trigonometric ratio is given as SOH CAH TOA
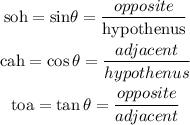
now, let's use the formula of tangent to solve this problem
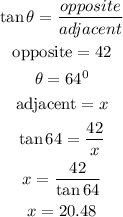
from the calculations above, the value of x is equal to 20.48