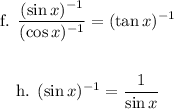Question

Determine if f, g, and h are true or false. If false, correct the statement with an explanation

Answer 1

We need to determine if the statements are true or false.

In order to do so, we need to pay attention to the following notations:

`\begin{gathered} (\sin x)^(-1)=(1)/(\sin x) \\ \\ \sin^(-1)x=\text{ inverse function of }\sin x \end{gathered}`

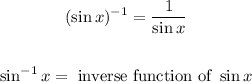
The same notations apply to cosine and tangent functions.

The inverse f⁻¹(x) is the function such that:

`(f^(-1)\circ f)(x)=f^(-1)(f(x))=x`

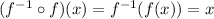
Thus, we have:

`\cos^(-1)(\cos((15\pi)/(6)))=(15\pi)/(6)`

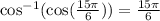
Therefore, statement g. is true.

In order to show that statements f. and h. are false, let's see what happens for x = 1/2:

`\begin{gathered} (\sin^(-1)((1)/(2)))/(\cos^(-1)((1)/(2)))=((\pi)/(6))/((\pi)/(3))=(3)/(6)=0.5\text{ \lparen no units\rparen} \\ \\ \tan^(-1)((1)/(2))\cong0.46\text{ \lparen rad\rparen} \\ \\ \Rightarrow(\sin^(-1)((1)/(2)))/(\cos^(-1)((1)/(2)))\\e\tan^(-1)((1)/(2)) \end{gathered}`
`\begin{gathered} \sin^(-1)((1)/(2))=(\pi)/(6)\cong0.52 \\ \\ (1)/(\sin((1)/(2)))\cong2.09 \\ \\ \Rightarrow\sin^(-1)((1)/(2))\\e(1)/(\sin((1)/(2))) \end{gathered}`

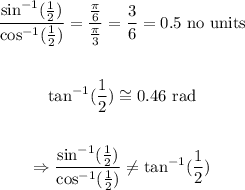
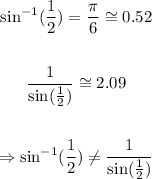
Answer:

f. False

g. True

h. False

Notice that we can correct the statements f. and h. by using the correct notation:

`\begin{gathered} \text{ f. }((\sin x)^(-1))/((\cos x)^(-1))=(\tan x)^(-1) \\ \\ \text{ h. }(\sin x)^(-1)=(1)/(\sin x) \end{gathered}`