Question

The tables of ordered pairs represent some points on the graphs of lines q and v. Line 9 Line v Х -9 -3 2. Х 0 10 у 0 18 33 у 10 8 3 Which system of equations is represented by lines q and v? F 21x - y = 9 5x + 6y = 40 G 3x - y = -27 x + 2y = 16 H 21x - y = 9 5x - 6y = 20 3 9x - y = -27 x + 2y = 8

Answer 1

One of the forms we can write the equation of a line is like this:

y - y1 = m(x - x1)

Where (x1, y1) is a point where the line passes through, and the value of m, the slope of a line is given by the following formula:

`m=(y2-y1)/(x2-x1)`

Then, for the first line (line q), we can take the points (-9, 0) and (-3, 18), then we get:

`mq=(18-0)/(-3-(-9))=(18)/(-3+9)=(18)/(6)=3`

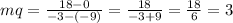
By replacing the value of the slope and the coordinates of the point (-9, 0), we get:

y - 0 = 3(x - (-9))

y = 3(x + 9)

y = 3x + 27

y - y = 3x + 27 - y

0 = 3x + 27 - y

-27 = 3x + 27 - 27 - y

-27 = 3x - y

For line v, we can take the points (-4, 10) and (0, 8), then we get:

`mv=(8-10)/(0-(-4))=(-2)/(4)=-(1)/(2)`

By taking -1/2 for the slope and the coordinates of the point (0,8), we gat:

y - 0 = -1/2(x - 8)

y = -1/2x + 4, multiplying both sides by 2:

2y = -x + 16

2y + x = -x + x + 16

2y + x = 16

Then, the system represented by the lines q and v is option G