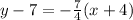Question

Write in point slope form the equation for the line that goes through the points (0,0) and (-4,7)

Answer 1

PROBLEM:

To find the point-slope form of the equation of the line passing through points (0, 0) and (-4, 7)

METHOD:

The point-slope form of the equation of a line is given to be:

`\begin{gathered} (y-y_0)=m(x-x_0) \\ \text{where} \\ m=\text{ slope} \\ (x_0,y_0)=\text{ Point on the line} \end{gathered}`

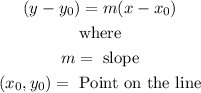
Step 1: Find the slope of the line.

The formula to calculate the slope of a line is given to be:

`m=(y_2-y_1)/(x_2-x_1)`

We can use the two points provided to find the slope of the line such that:

`\begin{gathered} (x_1,y_1)=(0,0)_{} \\ (x_2,y_2)=(-4,7) \end{gathered}`

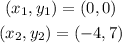
Therefore, the slope is given to be:

`\begin{gathered} m=(7-0)/(-4-0) \\ m=-(7)/(4) \end{gathered}`

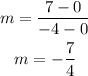
Step 2: Pick a point on the line to use for the equation.

`(x_0,y_0)=(-4,7)`

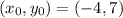
Step 3: Use the values gotten from Steps 1 and 2 to write out the equation of the line in the point-slope form:

`\begin{gathered} \Rightarrow y-7=-(7)/(4)(x-\lbrack-4\rbrack) \\ \therefore \\ y-7=-(7)/(4)(x+4) \end{gathered}`

ANSWER:

The slope-intercept form of the line is given to be:

`y-7=-(7)/(4)(x+4)`