Question

In the diagram below of triangle DEF, G is a midpoint of D E and H is a midpointof EF. If MZGHE = x + 52, and mZDFH = 96 – 102, what is the measureof ZDFH?

Answer 1

According to the given figure, angles GHE and DFH are corresponding angles, which are equal because GH and DF are parallels. So, we can express the following

`m\angle GHE=m\angle DFH`

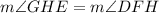
Replacing the given expressions, we have

`x+52=96-10x`

Let's solve for x

`\begin{gathered} x+10x=96-52 \\ 11x=44 \\ x=(44)/(11) \\ x=4 \end{gathered}`

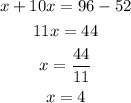
Then, we find the measure of the angle DFH

`\begin{gathered} m\angle DFH=96-10x=96-10\cdot4=96-40 \\ m\angle DFH=56 \end{gathered}`

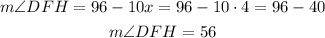
Hence, the angle DFH measures 56°.