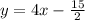Question

Determine an equation of the line that is perpendicular to the tangent to the graph y=1/x at x=2 and intersects at the point of tangency.

Answer 1

`y=4x-(15)/(2)`

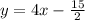
Step-by-step explanation

Two lines are perpendicular if they have opposite reciprocal slopes. So, to find the line, first, we have to find the slope of the line tangent to the graph of y = 1/x at x = 2. To do so, we have to find the derivative of the function and evaluate it at x = 2. That is the slope of the tangent line at that point.

The derivative of the function is,

`y^(\prime)=\left((1)/(x)\right)^(\prime)=(x^(-1))^(\prime)=-1\cdot x^(-1-1)=-1x^(-2)=-(1)/(x^2)`

So, the slope of the tangent line at x = 2 is,

`y^(\prime)(2)=-(1)/(2^2)=-(1)/(4)`

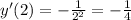
Therefore, the slope of the perpendicular line is the opposite reciprocal,

`m=-(1)/(y^(\prime)(2))=-(1)/(-(1)/(4))=4`

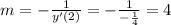
So we have that the perpendicular line we are looking for is,

`y=4x+b`

We have to find the y-intercept, b. We know that this perpendicular line intersects the graph at the tangency point, so with that point, we will find b.

The x-coordinate of the tangency point is x = 2, and the y-coordinate is,

`y(2)=(1)/(2)`

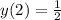
Substitute (x, y) with (2, 1/2) in the equation of the line to find b,

`\begin{gathered} (1)/(2)=4\cdot2+b \\ \\ (1)/(2)=8+b \end{gathered}`

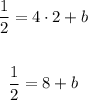
Subtract 8 from both sides,

`b=(1)/(2)-8=(1-8\cdot2)/(2)=(1-16)/(2)=-(15)/(2)`

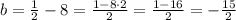
Hence, the equation of the line perpendicular to the tangent of the graph at x = 2 passing through the tangency point is,

`y=4x-(15)/(2)`