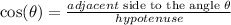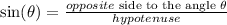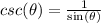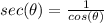Step-by-step explanation:
Consider the following right triangle:
In this triangle
x = adjacent side to the angle theta.
y = opposite side to the angle theta.
h= hypotenuse.
Now, by definition, we have the following trigonometric ratios:
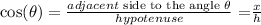


and according to the above trigonometric ratio, we get:

On the other hand, we get the following reciprocals:
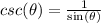
and
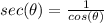
we can conclude that the correct answer is:
Answer:
The six trigonometric ratios: