Question

Find the x-intercepts of the polynomial y = a2 + 16a + 64

Answer 1

Given the polynomial:

`y=a^2+16a+64`

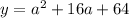
The x-intercepts are the points in which the polynomial crosses the x-axis. That is, are the points (x, 0).

To find these points, use the quadratic formula according to the steps below.

Step 01: Substitute the values in the quadratic formula.

For a equation y = ax² + bx + c, the x-intercepts are:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this question,

a = 1

b = 16

c = 64

Substituting the values:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-16\pm\sqrt[]{16^2-4\cdot1\cdot64}}{2\cdot1} \end{gathered}`

Step 02: Solve the equation above.

Begin by solving the square and the multiplications:

`x=\frac{-16\pm\sqrt[]{256^{}-256}}{2}`

Now, subtract the values inside the root.

`x=\frac{-16\pm\sqrt[]{0}}{2}`

Solve the root:

`x=(-16\pm0)/(2)`

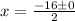
And find the values of x:

`\begin{gathered} x_1=(-16-0)/(2)=-(16)/(2)=-8 \\ x_2=(-16+0)/(2)=-(16)/(2)=-8 \end{gathered}`

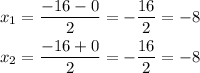
Answer: The x-intercepts are: (-8, 0), (-8, 0).