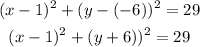Answer:
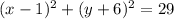
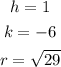
Step-by-step explanation:
Given:
Endpoints of the diameter of a circle as (-4, -8) and (6, -4)
To find:
Equation of a circle in standard form
The equation of a circle in standard form is generally given as;
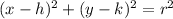
where (h, k) is the coordinate of the center of the circle and r is the radius of the circle.
We'll go ahead and determine the coordinates of the midpoint of the endpoints of the diameter which will be the coordinates of the center of the circle as seen below wi;
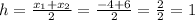
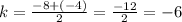
So the center of the circle has coordinates (1, -6)
Since h = 1, and k = -6 and we have that x1 = -4 and y1 = -8, we can go ahead and solve for r as seen below;
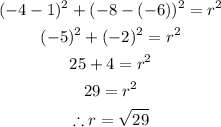
We can now write the equation of the circle in standard form as;