Given data:
The diagonals of rhombus d1 = 15 in and d2 = 20 in
The area of the rhombus,
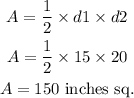
Now, to find the perimeter of rhombus we first find the side of rhombus.
The diagonal of the rhombus is considered as diameter, so the radius will be
d1 = r1 = 7.5
d2 = r2 = 10
So, by using the pythagorean theorem we find the side of the rhombus
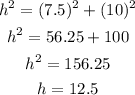
The perimeter of the rhombus is,
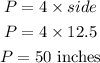
Thus, the area is 150 in. sq. and perimeter is 50 in.