Question

Suppose Rachel and Nadia buy a house and have to take out a loan for $183500. If they qualify for an APR of 3.75% and choose a 30 year mortgage, we can find their monthly payment by using the PMT formula. If Rachel and Nadia decide to pay $1500 per month, we can use goal seek to see how many years it will take to pay off the loan. Use the PMT function and goal seek (as needed) to answer the following questions about Rachel and Nadia's mortgage. a. What is their monthly payment on the 30 year loan? $ 15 year loan, what will the new monthly payment be?

Answer 1

We have that the PMT formula is given by:

`\text{PMT}=p(((r)/(n))/(1-(1+(r)/(n))^(-ny)))`

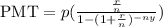
Where p is the initial principal (Loan ammount), r is the interest rate period, n is the total number of payments or periods, y is the number of years, PMT is the monthly payment.

Now, replacing the data in the formula, we will get:

*The payment will be due for 30 years, that is 12 months each year [That is our n] and y will be 30, r is 0.0375.

p will be $183500, that is:

`\text{PMT}=(183500)(((0.0375)/(12))/(1-(1\pm(0.0375)/(12))^(-(12)(30))))`

Then, we will have that the monthly payment for the 30 years, should be:

`\text{PMT}=849.8171105`

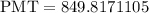
If she wishes to pay $1500 each mothn, we then replace in the formula:

`1500=(183500)((((0.0375)/(12)))/(1-(1+(0.0375)/(12))^(-12y))`

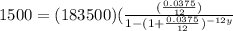
Now, solving for Y, we will have:

`-12y=(\ln((593)/(960)))/(\ln((321)/(320)))\Rightarrow y\approx12.86643229`

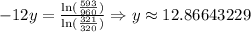
From this, we have that if they pay a monthly morgage of 1500, they would take 13 years to pay the total cost.

If they wanted to pay the morgage in 15 years, then we replace in the formula as follows:

`\text{PMT}=(183500)((((0.0375)/(12)))/(1-(1\pm(0.03755)/(12))^(-12(15))))`

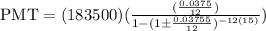
That is:

`\text{PMT=1334.453182}\Rightarrow PMT\approx1334.45`

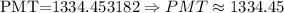
They would have to pay $1334.45 each month in order to pay the morgage in 15 years.