2.2.30QuesticFind a quadratic function that includes the set of values below.(0,6), (2,8), (3,0)The equation of the parabola is y=0

Question

asked Oct 25, 2023 96.7k views

1 Answer

Wibbly · Answer 1 · 2023-10-31T05:35:33+0000

The form of quadratic is:

Since (0,6) is given, we know c = 6, thus we have:

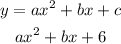
$\begin{gathered} y=ax^2+bx+c \\ ax^2+bx+6 \end{gathered}$

Point 2 is (2,8), replace x and y and find equation:

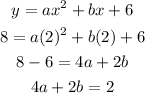
$\begin{gathered} y=ax^2+bx+6 \\ 8=a(2)^2+b(2)+6 \\ 8-6=4a+2b \\ 4a+2b=2 \end{gathered}$

Putting point 2 (3,0), we have:

$\begin{gathered} y=ax^2+bx+6 \\ 0=a(3)^2+b(3)+6 \\ 9a+3b=-6 \end{gathered}$

Solving the 2 simulatenous equations for a and b, we get:

a = -3

b = 7

Now u have all the values, a, b, and c.

Just put it in the general form of parabola :

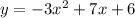
y = -3x^2 + 7x + 6