Inequalities
Solve:
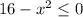
For a better understanding, we first multiply the inequality by -1. Recall by doing so, the sign must be flipped:
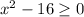
Factor the binomial:
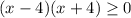
We have a product of two variable expressions and it must be positive or zero. That can only be possible if:
* Both factors are positive or zero
* Both factors are negative or zero
The answer can come from any of the conditions stated above, so the solution is the OR combination of the individual solutions.
The first condition states:
x - 4 ≥ 0 AND x + 4 ≥ 0
This leads to the solution:
x ≥ 4 AND x ≥ -4
If x must be greater or equal to 4 and greater or equal to -4, then the AND combination gives the solution: x ≥ 4
The second condition states:
x - 4 ≤ 0 AND x + 4 ≤ 0
This leads to:
x ≤ 4 AND x ≤ -4
The AND combination gives the second solution x ≤ -4
The final solution is the first solution OR the second solution, that is:
x ≤ -4 or x ≥ 4
Representing the solution in the number line, we get the graph below:
Expressed in interval form: (-∞ , -4] U [4, +∞)