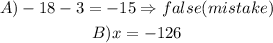
Step-by-step explanation
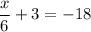
Step 1
to find the solution we need to isolate x, so
a)subtract 3 in both sides
so
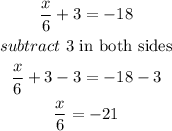
therefore, the mistake the student did is
he did :
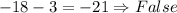
Step 2
now, to find the true value for x , let's continue with the solution
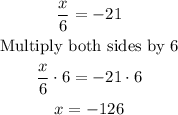
therefore, the answer is

I hope this helps you