Question

Jillian, a pro golfer, is practicing chip shots (shorter andslower swings). Jillian hits a golf ball off the ground with aninitial velocity of 50 ft/sec at an angle of elevation of 35°above the horizon. If the ball took approximately 1.792seconds to fall back to the ground, and it reached itsmaximum height halfway through its flight, what was itsmaximum height?

Answer 1

We'll assume the shot has a parabolic arc since we are told it reaches its maximum height midway through its flight.

The equation that describes its movement through the y axis is

`y=v_0\cdot\sin (\theta_0)\cdot t-(1)/(2)g\cdot t^2`

Where v₀ is the initial velocity, θ₀ is the initial angle and g is the force of gravity.

The equation that descibes its speed at any point in the y axis is

`v_y=v_0\cdot\sin (\theta_0)-g\cdot t`

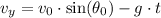
In order to find its maximum height, we need to find a point at which

`v_y=0`

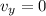
as that would mean the ball is no longer moving up or down. Let's keep in mind that the end of the trajectory would satisfy this condition, so let's dicard it right away.

In order to proeed we must consider the equation

`0=v_(0y)\cdot\sin (\theta_0)-g\cdot t`

We already have all the data we need in order to solve it, so let's plug in the given values