Answer:
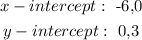
Explanation:
A linear equation is represented by the following equation:
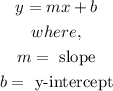
Therefore, if we re-organize the equation using the slope-intercept form, we can identify ''b'':
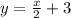
Therefore, the y-intercept of the function is (0,3).
Now, for the x-intercept, substitute y=0.
