Question

A bag contains 4 orange marbles, 6 blue marbles, 8 red marbles, 7 green marbles, and 2 white marbles. A marble is chosen at random, not replaced, then another marble is chosen.Find the P (orange,then white)

Answer 1

Given:

Number of orange marbles = 4

Number of blue marbles = 6

Number of red marbles = 8

Number of green marbles = 7

Number of white marbles = 2

Required: Probability of choosing orange marble then white marble

Explanation:

Total number of marbles

`\begin{gathered} =4+6+8+7+2 \\ =27 \end{gathered}`

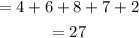
Probability of choosing first marble as orange marble =

`\begin{gathered} =\frac{\text{ Number of orange marbles}}{\text{ Total number of marbles}} \\ =(4)/(27) \end{gathered}`

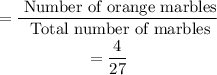
After selecting the first marble, the total number of marbles remaining is 27 - 1 = 26.

Probability of choosing a white marble as the second marble

`\begin{gathered} =\frac{\text{ Number of white marbles }}{\text{ Total number of marbles remaining}} \\ =(2)/(26) \end{gathered}`

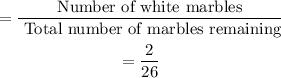
So, P(Orange, then white)

`\begin{gathered} =(4)/(27)\cdot(2)/(26) \\ =(8)/(702) \end{gathered}`

Final Answer: P(Orange, then white) = 8/702