We have to write the system of equations and find the solution.
Our variables are the miles of each car in one week, so we call x for car 1 and y for car 2 the miles that each car drove.
One equation is that the two cars drove a combined total of 975 miles, so:
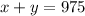
And the other equation, is that ths sum of their fuel efficiences are 35 miles per gallon. Also, we know that car 1 consumed 25 gallons in one week and car 2 consumed 30 gallons on one week, so:
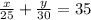
To find the solution we can isolate x from the first equation and replace into the second equation:
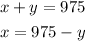
Replacing into second equation and isolate y:
![undefined]()