We have the graphs of the functions
f(x) ------ the left graph in the picture
g(x) ----- the right graph in the picture
We need to find
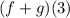
This means we need to find
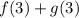
To find f(3) look at the left graph
Look for the value of y at x = 3
At x = 3 the value of y is 0, then
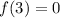
To find g(3), look at the right graph
Look for the value of y at x = 3
At x = 3 the value of y is 0, then
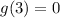
Add them
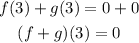
a)
(f + g)(3) = 0
We need to find
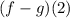
That means we need to find

To find f(2) look at the left graph
Look for the value of y at x = 2
At x = 2 the value of y is 1, then
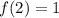
To find g(2) look at the right graph
Look for the value of y at x = 2
At x = 2 the value of y is 4, then
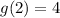
Subtract them
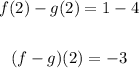
b)
(f - g)(2) = -3