Question

Use implicit differentiation to justify both horizontal asymptotes for the curve

Answer 1

Given the equation of the curve:

`y^2=x^3+3x^2...(1)`

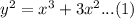
Using implicit differentiation:

`\begin{gathered} 2y\cdot(dy)/(dx)=3x^2+6x \\ \\ (dy)/(dx)=(3x^2+6x)/(2y) \end{gathered}`

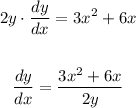
For the points with the slope equal to 0, we have:

`(dy)/(dx)=0`

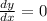
Using the expression above:

`\begin{gathered} (3x^2+6x)/(2y)=0 \\ \\ (3x(x+2))/(2y)=0 \end{gathered}`

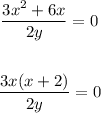
The apparent solutions are x = 0 and x = -2, but if x = 0, then y = 0 (using equation (1)), so we have an indetermination of 0/0. Then, the only solution is x = -2. Using this solution on (1):

`\begin{gathered} y^2=(-2)^3+3(-2)^2=-8+12=4 \\ \\ \Rightarrow y=2\text{ or }y=-2 \end{gathered}`

And this result is consistent with the graph.