Question

How do you answer questions about log

Answer 1

The ball is dropped from a height of h feet and repeatedly bounces of the floor

Since it reaches 2/3 of the height, we have

`\begin{gathered} h\text{ initial height dropped + } \\ 2h*(2)/(3)\text{ that is up and down with }(2)/(3)\text{ of h} \end{gathered}`

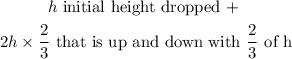
The second bounce becomes

`\begin{gathered} 2((2)/(3))h \\ \\ \end{gathered}`

So the bounces follow the series

`h+2((2)/(3))h+2((2)/(3))^2h+2((2)/(3))^3h+2((2)/(3))^4h+2((2)/(3))^5h`

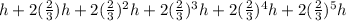
where a the first term = h

and r the common ratio = 2/3

So the total number of feet the ball travels between the first and sixth bounce is

`\sum_{i\mathop{=}1}^5(2h)((2)/(3))^i`

Hence the answer is option A