The given equation is:
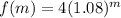
Where m is the number of months and f(m) is the length of the fish in cm.
a. When the study ended the function had a value f(m)=6.86 cm.
To find the domain for the growth function, we need to equal the equation to 6.86 and solve for m, as follows:

Thus, a reasonable domain to plot the growth function is (0,7).
b. The y-intercept of the graph of the function f(m) represents the length of the fish when the study started.
c. The average rate of change of an exponential function is given by the following formula:

Where (x1, y1) and (x2,y2) are the coordinates of the points at m=3 and m=7.
First, let's solve the function at m=3:

When m=7:
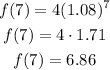
Thus the coordinates are (3,5.04) and (7,6.86), by replacing these values in the formula we obtain:

The average rate of change is 0.45 in the interval (3,7). It represents the growth rate in cm per month.