There are p=5 women and q=9 men.
6 people have to be chosen and out of it more than 3 must be men.
So, the people can be chosen as:
• 4 men and 2women
or
• 5 men and 1 woman
or
• 6 men and no woman.
So, the number of ways of choosing 6 people if more than 3 must be men is,
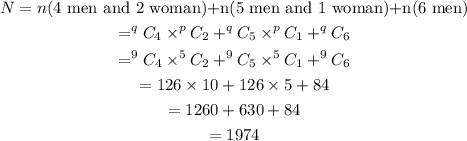
Therefore, there are 1974 ways of choosing 6 people if more than 3 must be men.