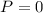There are a total of 10 balls in the box, which is the initial sample space of this problem. We have the keyword on the problem kept out of the box. This means that after getting a ball, the sample spaces will be reduced by 1 since we don't replace the ball that has been taken. This is the working concept for this type of problem.
1. For selecting 2 red balls, on the first round of picking, there are 3 red balls on the box out of 10 balls. The probability in this first picking is
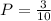
And after picking a red, there are 2 remaining red balls on the box and there are 9 remaining balls on the box. This probability now is represented as
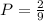
To get the overall probability, we just multiply these two probabilities. We get
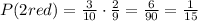
2. For selecting a blue ball and then a white ball, there are 2 blue balls on the box out of 10 balls. The probability in this first picking is
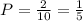
After picking a blue ball, there are 5 white balls on the box out of 9 balls. The probability of picking a white ball is represented as

To get the overall probability, multiply these two probabilities, getting
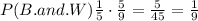
3. For selecting a red ball, the probability is already provided on item 1 which is
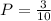
After picking the red ball, there are 2 blue balls on the box out of 9 balls. The probability of picking a blue ball is represented as
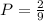
To get the overall probability, multiply these two probabilities, getting
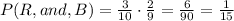
4. We only have 2 blue balls on the box. There is no chance that we can get three blue balls. Hence,